引言

勾股定理，也称为毕达哥拉斯定理，是数学中的一个基本定理，它描述了直角三角形中三边长度的关系。这个定理不仅在数学领域有着深远的影响，而且在工程、建筑、物理等多个领域都有着广泛的应用。本文将围绕勾股定理展开，探讨其历史、证明方法以及在实际问题中的应用。

勾股定理的历史背景

勾股定理最早出现在公元前2000年左右的古埃及，后来古希腊数学家毕达哥拉斯在公元前6世纪对其进行了深入研究。据传说，毕达哥拉斯学派发现了一个奇妙的性质：在一个直角三角形中，直角边的平方和等于斜边的平方。这个发现引起了人们的极大兴趣，并逐渐演变成了勾股定理。

勾股定理的证明方法

勾股定理有多种证明方法，以下列举几种常见的证明方式：

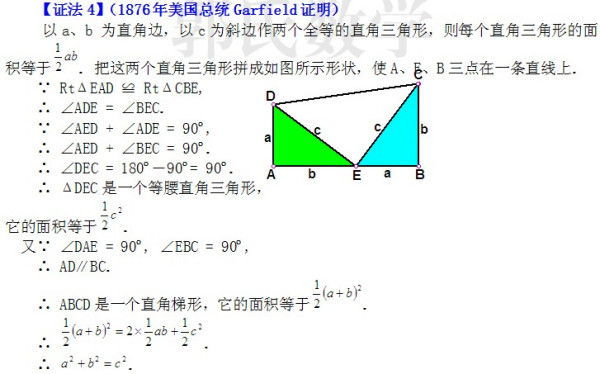
• 几何证明：通过构造几何图形，如将直角三角形的斜边分成两段，然后证明这两段与直角边构成的四个三角形全等，从而得出勾股定理。

• 代数证明：通过设定直角三角形的边长，建立方程组，然后解方程得出勾股定理。

  

• 数论证明：利用数论中的性质，如勾股数、完全平方数等，推导出勾股定理。

勾股定理的应用

勾股定理的应用非常广泛，以下列举几个例子：

• 建筑设计：在建筑设计中，勾股定理可以帮助工程师计算直角三角形的边长，确保结构的稳定性。

• 工程测量：在工程测量中，勾股定理可以用来计算距离，特别是在需要测量斜坡或地形高度的情况下。

  

• 物理学：在物理学中，勾股定理可以用来计算速度、加速度等物理量的合成。

• 数学竞赛：在数学竞赛中，勾股定理是必考内容，考生需要熟练掌握其证明和应用。

勾股定理的推广

勾股定理不仅仅适用于直角三角形，还可以推广到更一般的情况。以下是一些推广的例子：

• 勾股数：勾股数是指满足勾股定理的三元组，如(3, 4, 5)。这些数在数学和物理学中有着广泛的应用。

  

• 勾股树：勾股树是一种特殊的树形结构，其节点上的值满足勾股定理。

• 勾股矩阵：勾股矩阵是一种特殊的矩阵，其元素满足勾股定理。

结论

勾股定理是一个简单而又深刻的数学定理，它不仅揭示了直角三角形中边长之间的关系，而且在实际生活中有着广泛的应用。通过对勾股定理的学习和探究，我们可以更好地理解数学的美丽和力量。在未来，勾股定理将继续在各个领域发挥着重要作用。